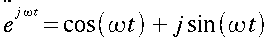
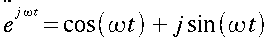
Inhalt des Brückenkurses »Mathematik für Studenten der Elektrotechnik, Informationstechnologie oder Sicherheitstechnik«
Elementares Rechnen (Bruchrechnung, Potenzen und Logarithmen, einfache Gleichungen und Ungleichungen)
Vektorrechnung und analytische Geometrie
Vektorielle Beschreibung von Geraden und Ebenen sowie von Flugparabeln, Schnittmengenbstimmung
Lineare Gleichungssysteme, Löungsverfahren und allgemeine Eigenschaften
Skalarprodukt und Vektorprodukt
Komplexe Zahlen (Grundrechenarten mit kartesischen und Polarkoordinaten)
Umgang mit Funktionen (Analysis)
Eigenschaften der Grundfunktionen (Potenzfunktionen, Exponentialfunktion und trigonometrische Funktionen)
Ableitungskalkül (insbesondere Quotienten- und Kettenregel), auch vektorielle Geschwindigkeit
Integrationstechnik
Kurs Frühjahr 2006 vom 1.-31.3. 2006
Übungen: ... Nr.1 ... Nr.2 ... Nr.3 ...Nr.4 ... Nr.4b ... Nr.5 .... Nr.6 ... Wo.2 ....Nr.7 ... Nr.8 ... Nr.9 ... Nr.10
Lösungen:... Nr.1 ... Nr.2 ... Nr.3 ... Nr.4 ... Nr.4b ... Nr.5 .. Nr.6 ... Wo.2 ... Nr.7 ... Nr.8 ... Nr.9 .. Nr.10
Übungen: .... Wo.3 ... Nr.11 ... Nr.12 ... Nr.13 ... Nr.14 ... Wo.4 ... Nr.15
Lösungen: .. Wo.3 ... Nr.11 ... Nr.12 ... Nr.13 ... Nr.14 .... Wo.4 ... Nr.15
Klausur: Mittwoch d. 29.3. von 9.00-13.00 Uhr in FH1 Campus Freudenberg.
Alle üblichen Hilfsmittel zugelassen, schaden aber erfahrungsgemäß eher als zu nutzen.
Übungen Sommer / Herbst 2005
Übung: 1.Woche ............... 2. Woche ..............3.Woche 3.Wochenende 4. Woche 4.Wochenende .. 5.Woche
.......... Lösungen dazu ...... Lösungen dazu ......Lösungen dazu ................Lösungen dazu
Übungen Frühjahr 2005
Übung: 1.Woche 2. Woche 3.Woche 4. Woche Probeklausur/Wochenendaufgaben
Übungen Sommer 2004
Übung: - 1. Woche 2.Woche – 3.Woche – 4.Woche – 4. Wochenende u. 5. Woche
Lösung 1.Woche - Lösung 2.Woche – Lösung 3.Woche – Lösung 4. Woche -- Lösung 4. Wochenende --
Übungen Frühjahr 2004
Übung 1. Woche 2.Woche 3. Woche 4. Woche 5. Woche
Übungen Herbst 2003
Übungen Nr. 1 u. 2 Nr. 3 u. 4 u. Wochenende , Übungen 2. Woche , Übungen 3. Woche ,
Übungen Frühjahr 2003
1.Woche 2.Woche Logik 3.Woche 4.Woche 5.Woche
Übungen zum Kurs Herbst 2002
Übungen zum Kurs Frühjahr 2002
Übungen zum Kurs September 2001
Skriptum zum Kurs September 2001
Besonderheiten des Kurses
Die folgenden zentralen Inhalte des Kurses werden in den jeweiligen Mathematikveranstaltungen des ersten Semesters vorausgesetzt: Analytische vektorielle Geometrie in 2 und 3 Dimensionen, reelle Grundfunktionen (insbesondere trigonometrische), Kurvendiskussion, Ableitungs- und Integrationskalkül, elementares Rechnen mit komplexen Zahlen. Daher sollten alle Abiturienten am Kurs teilnehmen, die sich dafür schulisch unzureichend vorbereitet fühlen. Diese Gruppe stellte in den letzten Jahren bereits mehr als die Hälfte der Teilnehmer.
Materialien zum alten Kurs :
Zurück zur Übersicht