
Theoretische Teilchenphysik
Fakultät für Mathematik und Naturwissenschaften
Bergische Universität Wuppertal
D-42097 Wuppertal
Quarks on the Lattice
|
The force between two quarks is mediated by gluons. The reason why up to now no
free quarks could be observed is the following: the strong interaction is
increasing in strength with the distance between quarks. The strong interaction
can be described by a fundamental equation and is an important part of the
``standard model of particles''. This fundamental equation is based on only a
few underlying symmetry principles and can be used to explore the properties of
nuclear matter on the computer, i.e. to simulate a thermodynamically isolated
system of quarks and gluons and thus to analyze the behavior of quarks and
gluons in a virtually laboratory. This is possible by discretising the
fundamental equation.
See also the Budapest-Marseille-Wuppertal collaboration. |

|
Phenomenology of Elementary Particles
Our research focus is the prediction and interpretation of the phenomena observed at particle colliders. By relating experiment to theory, we try to get insight into the structure of elementary particles and their interactions.
Currently, our main interest is in physics at the Large Hadron Collider (LHC, CERN), the Tevatron (Fermilab), and a future International Linear Collider. Of particular importance at these machines is the search for and study of the last missing piece of the Standard Model: the Higgs boson. We also investigate the possibility of physics beyond the Standard Model, such as Supersymmetry.
The mathematical framework that we apply is perturbative Quantum Field Theory. Although its derivation is extremely complex, the essence of it can be formulated in a very intuitive way by so-called Feynman diagrams. Each Feynman diagram corresponds to a mathematical expression (involving multi-dimensional integrals in general). Its evaluation gives a numerical value for the scattering cross section which can be compared to experiment.
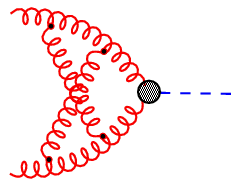
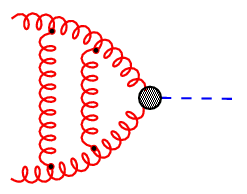
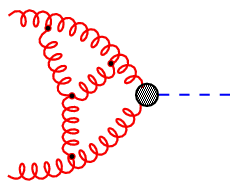
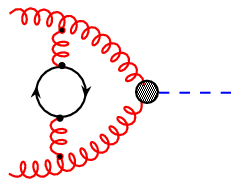
|
Figure 1: Feynman diagrams representing the fusion of two gluons into a Higgs boson. |
The number of loops in such diagrams reflects the order of perturbation theory. At higher orders, the evaluation of these diagrams becomes more and more complex and requires the development of new and efficient algorithms. Computer algebra plays a very important role in this respect.
As an example for the importance of loop diagrams (also termed radiative corrections), consider Fig.1 which shows the leading, next-to-leading, and next-to-next-to-leading order (or 0-, 1-, and 2-loop) result for the Higgs production cross section at the LHC.
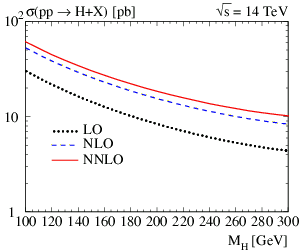
|
Figure 2: Leading (black dotted), next-to-leading (blue dashed), and
next-to-next-to-leading (red solid) order prediction for the production
cross section of a Higgs boson in the Standard Model (taken from PRL 88 (2002) 201801). |
Without the radiative corrections (dotted line), the cross section would be underestimated by roughly a factor of two.
See also here.

