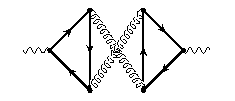|
|
|
|
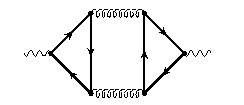
Home Brief CV – Research – Teaching Outreach Conferences Software Press Links Search Portal external: Higgs WG LHC and Philosophy | Research interests:Quark mass effects in higher order QCD - Asymptotic ExpansionsAsymptotic expansionsA central part of my Ph.D. thesis was concerned with the precise determination of the influence of finite quark masses to the hadronic cross section at electron-positron colliders. A powerful tool for this kind of calculations is provided by the method of asymptotic expansion, an effective re-formulation of the operator product expansion (for a review see [9]). Previously, the application of this procedure was restricted to lower orders of perturbation theory because it requires the evaluation of the huge number of diagrams generated by this approach. Therefore we automated the method which allowed to compute the third order QCD corrections to the hadronic R ratio as an expansion in the quark mass [8], [7] (for a review on the automatic computation of Feynman diagrams, see [6]).
Top quark production at a Linear ColliderIt turned out that using the same strategy one could also examine top quark pair production at a linear collider. If the energy is slightly above the threshold region (click here for a treatment of the threshold region itself), the top quark mass still influences the cross section significantly. A detailed investigation of the corresponding production cross section was performed in [5].
Higgs boson decayAlso the decay of (heavy) scalar or pseudo-scalar Higgs bosons into top quarks could be investigated. Although the current limits on a Standard Model Higgs mass rule out this decay, the existence of other, heavier scalars or pseudo-scalar particles as predicted, for example, in supersymmetric theories is well possible. In a certain mass range, top quark mass effects may have a significant influence on the decay rate. This dependence was studied in [4] with the help of asymptotic expansions and the tools developed at the first stage of my thesis.
Padé approximations (for singlet diagrams)(For a review on Padé approximations see here.) The results obtained through asymptotic expansions can be combined so that the corresponding cross sections or decay rates will be valid over the full energy range. This strategy was already known for non-singlet contributions, but in order to correctly account for axial-vector couplings one needs its generalization to singlet diagrams.
Quartic mass terms at alpha_s^3All the discussion above is concerned with mass corrections at order alpha_s^2. In the massless case, most of the quantities above are known up to order alpha_s^3. To obtain an estimate on the mass effects at this order, the above strategy of asymptotic expansion leads to four-loop diagrams that can not be solved in general. However, using renormalization group methods, one can derive the quadratic mass terms at order alpha_s^3 from the ones at alpha_s^2. If one aims for the quartic mass terms, one may follow a similar strategy. Operator product expansion in combination with renormalization group methods allows to reduce the four-loop diagrams to three-loop ones. The method is briefly described in [2], while the results are presented in [1].Literature:
Robert Harlander: Research Interests -/- Home -/- TTP Karlsruhe -/- CERN Theory -/- HET Brookhaven last modified: Jan 5, 2004, by RH
|