Kommentar
Die (positive) Wurzel unserer Funktion f ergibt den Amplitudenfaktor W aus Aufgabe (15). Beachten Sie,dass f(x)³0 gilt. Da die positive Wurzel monoton wachsend ist, hat W an denselben Stellen Extremwerte wie f. Nur die Werte müssen entsprechend modifiziert werden.
Für den Amplitudenfaktor W aus Aufgabe (15) erhält man daher die generelle Ungleichung
![]() .
.
Setzt man weiter A+B=a und A-B=b für A,B>0, so folgt 2a=A+B und 2b=A-B. Wie sieht die zugehörige Ungleichung aus? Man erhält:
![]() .
.
Zum Beweis kann man wie folgt rechnen:
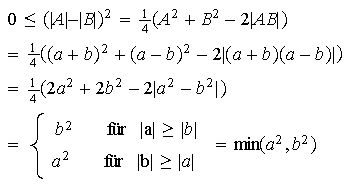
Da die positive Wurzel betrachtet wird, folgt die angegebene linke Ungleichung. Für die rechte Ungleichung rechnen wir entsprechend:
