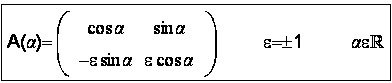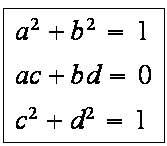
Lösung

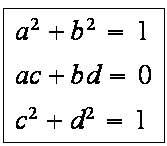
Wir wollen d über die 2. Gleichung eliminieren. Das erfordert eine Fallunterscheidung:

1.Fall: b=0. Also a²=1. Die 2. Gleichung lautet ac=0. Wegen a²=1 folgt c=0. Und damit d²=0. Das gibt insgesamt folgende 4 Lösungen des Systems mit b=0, wobei wir die Lösung in Matrixform schreiben.

2.Fall: b≠0. Jetzt eliminieren wir d mit Hilfe der mittleren Gleichung. Das gibt:

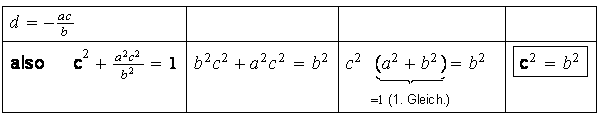
Für a,b und d verbleiben die erste und die umgeformte dritte Bedingung. (Zwei Gleichungen). Subtraktion der beiden Gleichungen gibt eine Gleichung für a und d, womit das Ende der Elimination erreicht ist.

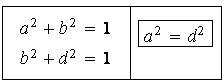
Jetzt kommt der bereits angedeute Trick. Wir parametrisieren die vorletzte Gleichung a²+b²=1 und legen dann durch Rückeinsetzen die übrigen Größen fest. Das gibt (als notwewndige Bedingungen an unsere Unbestimmten)

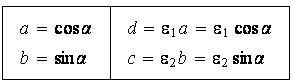
Dabei stehen die beiden ε wieder für mögliche Vorzeichen. Die erste und die letzte Gleichung ist hierdurch stets erfüllt. Wie steht es mit der mittleren? Einsetzen gibt: (ε₂+ε₁)ab=0. Also entweder a=0 oder ε₂+ε₁=0. Es zeigt sich, dass der erste Fall ebenso wie die 4 oben gefundenen Lösungen vom Fall ε₂+ε₁=0 mit erfasst werden. D.h. Man hat folgende Lösungen des ursprünglichen Systems (und das sind alle Lösungen):

Zurück