Lösung
Die beiden Geraden zu ε bzw. zu ε+Δε sind beide zu parametrisieren. Die Parameter seien u und v mit Schnittwerten uS und vS . Beide Schnittwerte hängen aber von Δε ab. Da ergibt folgende Schnittpunktsbedingung:
Das ist bereits die Schnittpunktsbedingung: Gesucht sind die Parameter uS und vS , die diese Vektorgleichung erfüllen! Jetzt entwickeln wir alle von Δε abhängigen Größen um Δε=0, bilden die zugehörige Tangentenzerlegung und setzen das in die Bedingungsgleichung ein.
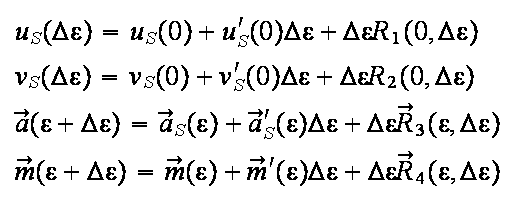
Das sieht viel aus, ist aber immer nur einfachstes Hinschreiben. Jetzt folgt das Einsetzen in die Bedingung. Wir sortieren nach Potenzen von Δε. Einiges hebt sich fort. Es bleibt:
Die
Argumente in den Resten haben wir fortgelassen. Wir Δε
nach Null gehen lassen. Das gibt sofort
.
Dabei nehmen wir an, dass
gilt.
Nach Einsetzen kann man ein Δε kürzen. Danach erneut Δε nach Null gehen lassen gibt:
oder
Wir erinnern
uns daran: Gesucht ist uS(0)=vS(0). Die zur
rezipokrn Basis führende Idee aus Kap.6.3 bringt uns sofort ans
Ziel. Zunächst müssen wir annehmen, dass
gilt. Nun suchen wir uns einen Vektor
,
der senkrecht auf
Nun multiplizieren wir unsere Bedingung skalr mit diesem Vektor und
finden sofort für die gesuchte Größe:
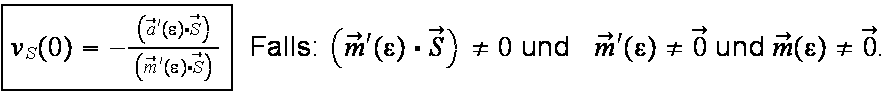
Einsetzen in die Parametrisierung gibt den gesuchten Grenzschnittpunkt
