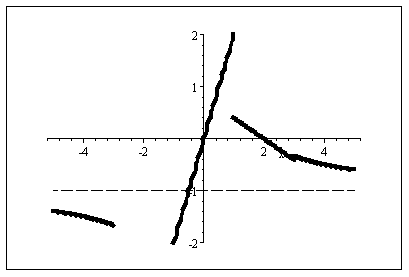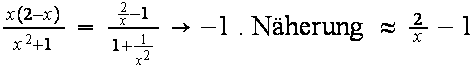
Inspektion

Was fällt bei der Inspektion des Rechenausdrucks sofort ins Auge: Eine rationale Funktion mit Nullstellen bei x=0 und x=2. Nenner 1+x² wird nie Null, ist immer echt positiv, g ist für alle x definiert. Eine Symmetrie ist nicht erkennbar.

Also wird das Vorzeichen durch das Vorzeichen des Zählers bestimmt. Positiv nur für 0<x<2.

Noch zu suchen: a) Dominanzverhalten bei den beiden Nullstellen. Leicht mit der Regel aus (8.3.31). Man erhält als dominante Beiträge 2x bei x=0 und 2/5(2-x) bei x=2

b) Verhalten für große |x| ? Umformung des Integranden anstreben, Polynomdivision.

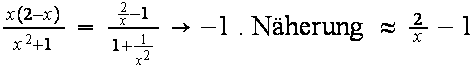
Asymptote füt große |x| ist y=-1.

c) Zwischen 0 und 2 muss ein Extremwert (Maximum!) liegen. Dazu die Ableitung mit der Quotientenregel bestimmen. Weitere Extremstellen? Für x<0 muss es ein Minimum geben.

Die Skizze stellt die so gefundene Information zusammen. Die halbquantitative Skizze sollte klar sein. Man erwartet ein Minimum bei x=-2 und ein Maximum bei x=0.5 sowie einen Wendepunkt bei 0. Je ein weiterer Wendepunkt rechts vom Maximum und links vom Minimum.

Zurück