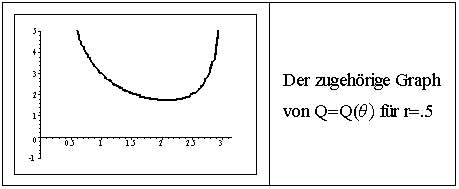
Kurvendiskussion
der Funktion
einschließlich Grenzfalldiskussion
Auflösen dieser Funktion nach cosq bzw sinq.
Behandlung physikalischer Zusatzfragen, wie die nach dem kleinstmöglichen Abtrieb oder der schnellsten Überfahrt.
Kommentar
Zu (Z3).
Zahlreiche Anschlussfragen liegen nahe. Z.B. : Welche Punkte des gegenüberliegenden Ufers kann man erreichen, wenn die skalare Bootsgeschwindigkeit v festliegt? Kann man insbesondere den Punkt mit A=0 (kein Abtrieb) erreichen. Das kann man entweder geometrisch oder über eine Kurvendiskusssion herausfinden. Dabei muss man die drei Fälle 0<r<1 und r=1 und r>1 für die Bootsgeschwindigkeit unterscheiden.
Diese Aufgabe verdeutlicht exemplarisch wesentliche Ziele der Ausbildung und damit des Vorkurses. Es geht umd das Verstehen und Lösen neuartiger und besonders auch komplexer Probleme. Dazu benötigt man verfügbares Wissen (Beispiel Vektoraddition der Kräfte), wirksame Lösungsstrategien (Beispiel Schnittmengenbestimmung wie im Vorkurs besprochen). Man sollte in der Lage sein, die Rechenschritte jeweils inhaltlich zu interpretieren und zu verstehen ( Beispiel: Das Auftreten von zwei Lösungen für den Einstellwinkel physikalisch, geometrisch und rechnerisch verstehen). Und man sollte über das Resultat nachdenken. Dazu stellen wir die (philosophische) Zusatzfrage: Häufig wird gesagt: Die Natur macht keine Sprünge. Was sagt unser Beispiel hierzu aus?
Einige Anschlussfragen, die mit den anspruchsvolleren Methoden des Vorkurses lösbar sind:
Kurvendiskussion
der Funktion
einschließlich Grenzfalldiskussion
Auflösen dieser Funktion nach cosq bzw sinq.
Behandlung physikalischer Zusatzfragen, wie die nach dem kleinstmöglichen Abtrieb oder der schnellsten Überfahrt.
Das Beispiel dieser Aufgabe sollte nicht als Abschreckung gesehen werden, „das kann ich nie“, sondern als Ansporn und Motivation.
Das Beispiel zeigt, was es bedeutet, wenn gesagt wird: Ein Physiker lernt neuartige und komplexe Probleme zu bearbeiten.
Wir liefern jetzt noch die geometrische Konstruktion des Einstellwinkels Ø bei gegebener skalarer Bootsgeschwindigkeit und erwünschtem Abtrieb A.
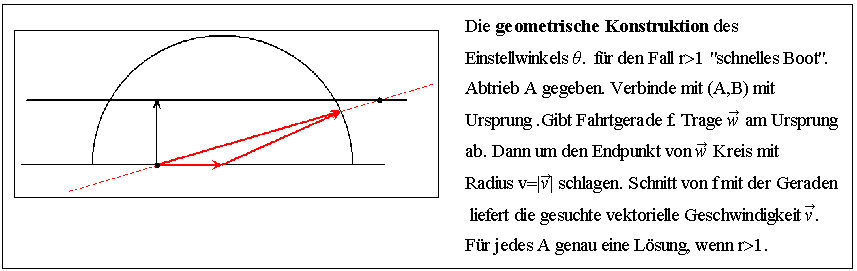
Alle
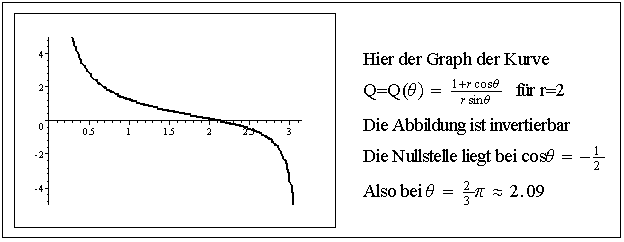
Abtriebswerte sind jetzt möglich. Die zugehörige Kurve
Q=Q(Ø) sieht in diesem Fall wie
wie folgt aus:
Und was ergibt sich für eine langsames Boot mit r<1? Zunächst die geometrische Konstruktion:
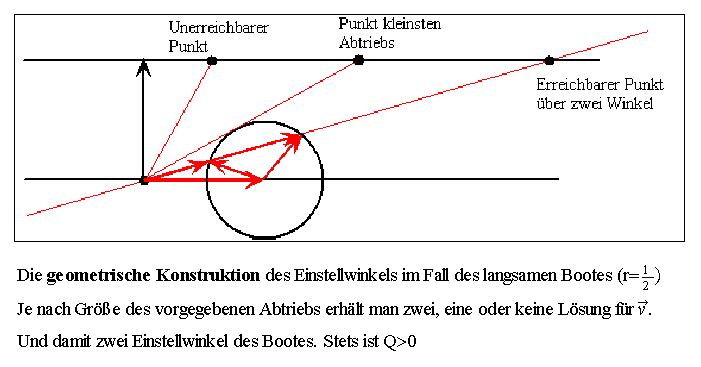
Jetzt sieht de Graph ganz anders aus. Ein typisches Beispiel zeigt das
