Inspektion
Der erste Teil der Aufgabe ist vornehmlich eine Wissensfrage: Vektorielle Geschwindigkeiten addieren sich unter den skizzierten Verhältnissen nach dem Parallelogramm der Kräfte, also in der Komponentenform koordinatenweise. Oder auch: Die im Skript mathematisch eingeführten Verknüpfungen dieser Vektoren repräsentieren auch die Vektoraddition der Geschwindigkeiten. Damit kann man die Geschwindigkeit des Bootes relativ zum Ufer bestimmen. Sie soll hier mit V bezeichnet werden. Ist diese Geschwindigkeit bekannt, kann man die Bahn des Bootes relativ zum Ufer angeben und deren Schnitt mit dem jenseitigen Ufer bestimmen.
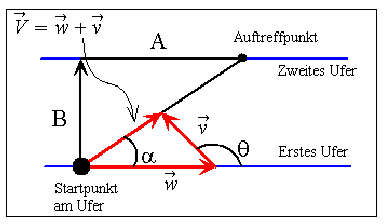
Auch hier sollte man mit einer Skizze starten, in der man die geometrische Konfiguration, aber auch die Geschwindigkeitsvektoren einzeichnet. Ein Punkt ist dabei zu beachten: Man sollte zur geometrischen Konstruktion der Bootsgeschwindigkeit relativ zum Ufer mit der Flussgeschwindigkeit (relativ zum Ufer) starten wie in der Figur, nicht mit der Bootsgeschwindigkeit relativ zum Fluss. Das Ergebnis sollte wie folgt aussehen:

Der gesuchte Auftreffpunkt ist der Schnittpunkt zweier Geraden. Man kann ihn geometrisch konstruieren oder aber vektoriell rechnerisch bestimmen. Beide Wege sind instruktiv.
Eine weitere Frage ist, wie man v festlegt. Durch die kartesischen Koponenten vx und vy oder polar durch Betrag v und Winkel q. Das ist der Winkel zwischen Fließrichtung und Bewegungsrichtung des Bootes vom Boot aus gesehen. Dagegen gibt a der Figur diesen Winkel vom Ufer aus gesehen! Jede solche Vorgabe entspricht einer anderen Präzisierung der Aufgabenstellung.
Interessant ist der Fall, das man die skalare Geschwindigkeit des Bootes relativ zum Wasser vorgibt. Also so etwas wie die Motorkraft. Welche Punkte des gegenüberliegenden Ufers kann man dann durch Variation von q ansteuern? Physikalisch anschaulich sollte klar sein, dass man mit einem langsamen Boot nicht alle Punkte erreicht.