Lösung
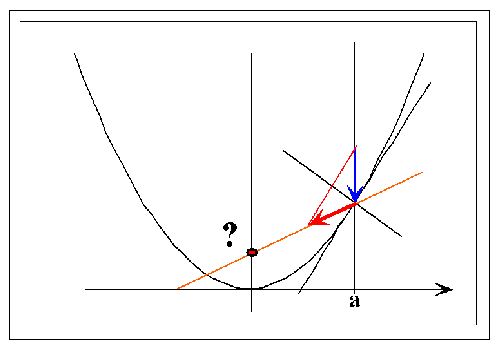
Wir wählen die Parabel mit Gleichung y=σx². Die Koordinaten y und x mögen dieselbe Einheit haben. Dann ist σx einheitenfrei, eine Zahl. Die Strahlen sollen parallel zur y-Achse verlaufen. Die Skizze fasst die Konfiguration zusammen. (Blau Richtungsvektor des einfallenden Strahles. Rot Richtungsvektor des reflektierten Strahles, gesucht der Schnittpunkt mit der y-Achse)

(2)
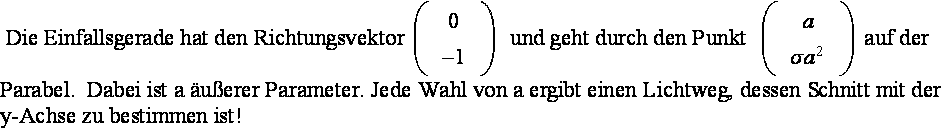
Die jetzt mögliche Geradenparametrisierung selbst benötigen wir nicht.
(3)

Mit Hilfe des allgemeinen Schemas kann man die zur Normalenrichtung n parallele Komponente der Einfallsrichtung e bestimmen:
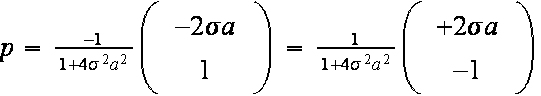
Das gibt für den reflektierten Strahl folgenden Richtungsvektor:
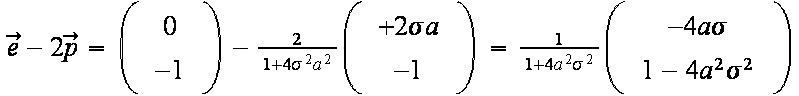
Da es nur auf die Richtung, nicht aber die Länge ankommt, können wir den Faktor 1/(1+4a²σ²) fortlassen und wählen als Richtungsvektor des reflektierten Strahles:
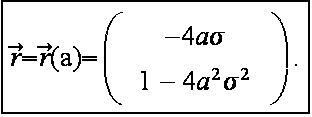
Damit ist Schritt 3 abgeschlossen! Man erhält als Parametrisierung der zum Parameter a gehörigen reflektierten Geraden:
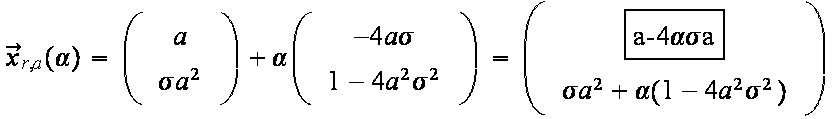
Wo trifft der reflektierte Strahl die y-Achse? Dazu muss der eingrahmte x-Weg den Wert Null haben (Merkmal der Punkte der y-Achse). Das bestimmt den α-Wert des Schnittpunktes zu
![]()
Einsetzen dieses Wertes in die zweite Koordinate gibt die gesuchte y-Koordinate, aus der erneut die a-Abhängigkeit herausfällt:
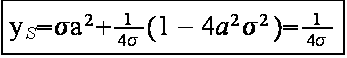
Also: Alle (an der Parabel y=σx²) reflektierten achsenparallelen Geraden schneiden sich in einem Brennpunkt mit Koordinatenvektor
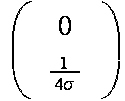 .
.
In diesem Beispiel kommt der Fokuspunkt als Schnittpunkt aller reflektierten Strahlen direkt heraus. Man benötigt keine spezielle Methoden der Infinitesimalrechnung zu seiner Bestimmung. Das ist untypisch einfach!