Aufgabe:

Der Fehler ist die Änderung, die man erhält, wenn man den wahren Wert durch eine Näherung ersetzt. Die unabhängige Veränderliche x ist hier in gewisser Weise diskret, zweiwertig. Dann hat man jeweils noch zu unterscheiden, ob man zur Beschreibung den absoluten oder den relativen Fehler verwendet.

Im Fall der Schwingungsdauer des Pendels ist die übliche Formel eine Näherung. Wie groß ist dann der Fehler, den man macht? Der maximale Winkel ist hier äußerer Parameter.

Wir haben für die Schwingungsdauer die folgende Näherungsformel höherer Ordnung

.

Dabei ist T₀ die übliche Näherung. Weiter sei T_i die Summe bis zur Potenz k²ⁱ. Dann tragen wir graphish (T_i-T₀)/T_i für die ersten i1,2,3 und 4 auf. Horizontal ist die maximale Winkelamplitude φ₀ aufgetragen. Das gibt folgendes Bild:

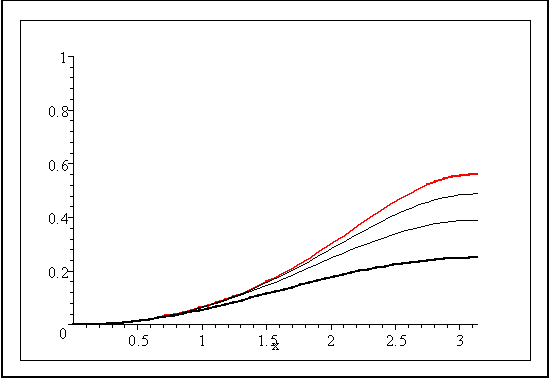
a) Wieso gehört die rote Kurve dann zu i=4?

b) Für φ₀=1 erhöht sich die Kurve bei Hinzunahme weiterer i nicht mehr sichtbar. Für φ₀ =3 dagegen erwtungsgemäß noch stark. Wie groß ist daher etwa der Fehler, den man macht, wenn man für φ₀=1 das wahre T durch die übliche Näherung ersetzt? Genauer: Welcher Fehler wird in der Figur dargestellt?

Inspektion -- Lösung -- Kommentar-

Zurück zur Liste der Aufgaben